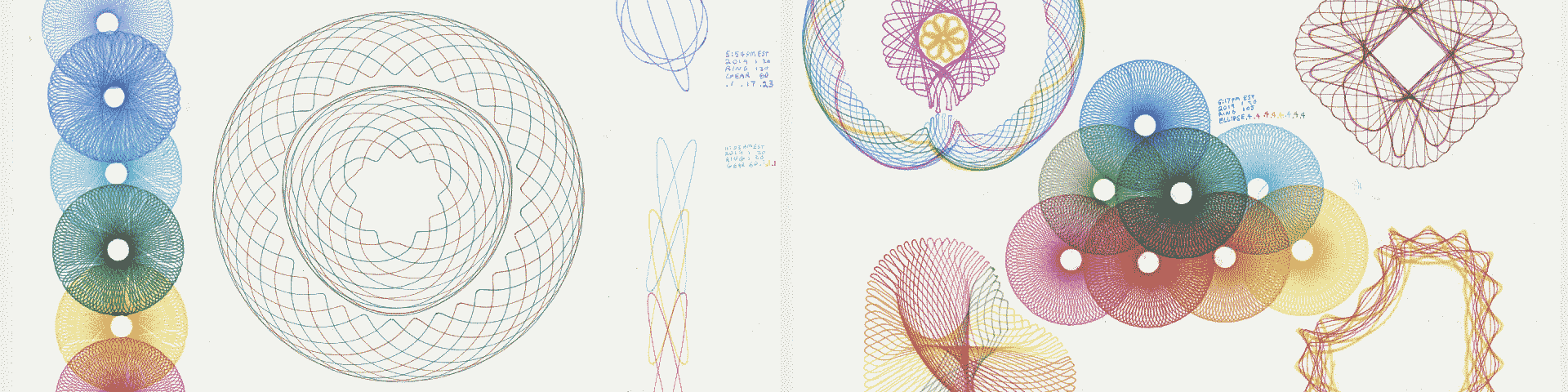
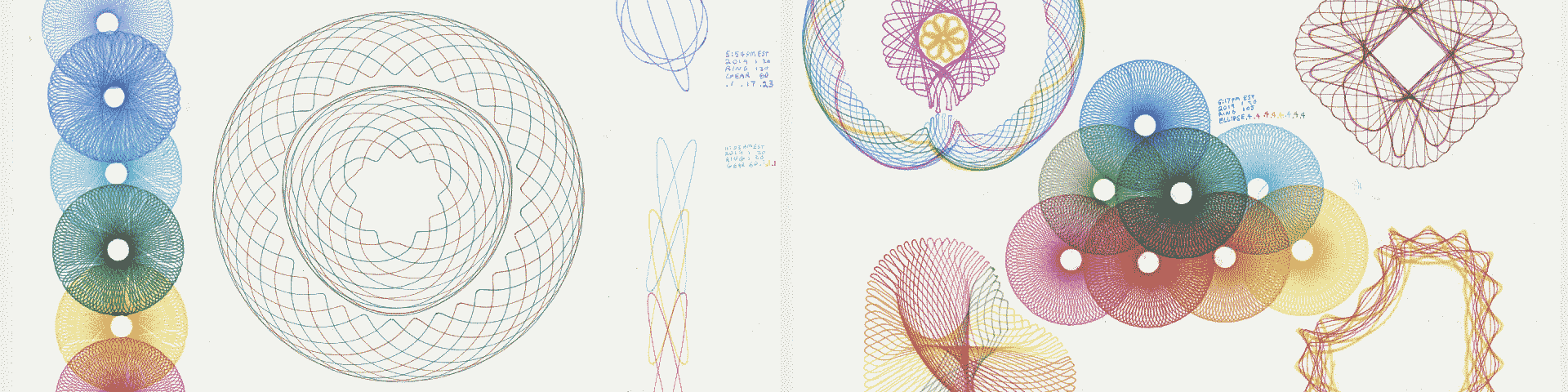
The trajectory of a point on the surface of the wheel that rolls on a straight surface without sliding.
Cycloid parametric equation: \[ \begin{cases} x = r(t-\sin{t}) \\ y = r(1-\cos{t}) \end{cases} \]
where \(r\) — radius of the circle, \(t\) — parameter.
The trajectory of a point on the surface of the wheel that rolls inside of another circle without sliding.
Hypocycloid parametric equation: \[ \begin{cases} x = (R - r) \cos t + r \cos(t - \frac{Rt}{r}) \\ y = (R - r) \sin t + r \sin(t - \frac{Rt}{r}) \end{cases} \]
where \(R\) — radius of the big circle, \(r\) — radius of the small circle, \(t\) — parameter.
The drawing point of the hypotrochoid is located at some distance from the center of the second wheel.
Hypotrochoid parametric equation: \[ \begin{cases} x = (R - r) \cos t + h \cos(t - \frac{Rt}{r}) \\ y = (R - r) \sin t + h \sin(t - \frac{Rt}{r}) \end{cases} \]
where \(h\) — distance to the drawing point, \(R\) — radius of the big circle, \(r\) — radius of the small circle, \(t\) — parameter.
The shape of the spiral depends on the ratio of the radii of the outer and inner wheels. This relation determines the shape of the hypotrochoid: \(k = \frac{R}{r}\)
If \(k \in \mathbb{N}\), the image resembles a star with the corresponding number of rays.
If \(k \in \mathbb{Q}\), meaning it can be represented as a fraction of integer numbers, then the image looks like a flower. And the numerator of the fraction determines the number of petals on this flower.
If the number \(k \in \mathbb{I}\), meaning that it cannot be represented as a fraction, then the curve is not closed, and a flower has an infinite number of petals.
The curves that the point draws on the surface of the outer wheel are called epicycloids, and at some distance from the center, epitrochoids.
Epicycloid parametric equation: \[ \begin{cases} x = (R + r) \cos t + r \cos(t + \frac{Rt}{r}) \\ y = (R + r) \sin t + r \sin(t + \frac{Rt}{r}) \end{cases} \]
Epitrochoid parametric equation: \[ \begin{cases} x = (R + r) \cos t + h \cos(t + \frac{Rt}{r}) \\ y = (R + r) \sin t + h \sin(t + \frac{Rt}{r}) \end{cases} \]
Derivation of the parametric equation of the epitrochoid:
If both circles are the same, the epitrochoid is called Pascal’s snail. Not after triangle-pressure-Pascal, but after his father.
Pascal’s snail parametric equation: \[ \begin{cases} x = 2r \cos t + r \cos(2t) \\ y = 2r \sin t + r \sin(2t) \end{cases} \]
We can add the third circle and get really beautiful spirals.
Epi-epitrochoid parametric equation (See proof) : \[ \begin{aligned} x & = (r_1 + r_2) \cos t + \\ & + (r_2 + r_3) \cos(t + \frac{r_1}{r_2}t - \frac{r_1}{p r_2}t) + \\ & + h \cos(t + \frac{r_1}{r_2}t - \frac{r_1}{p r_2}t - \frac{r_1}{p r_3}t); \end{aligned} \]
\[ \begin{aligned} y & = (r_1 + r_2) \sin t + \\ & + (r_2 + r_3) \sin(t + \frac{r_1}{r_2}t - \frac{r_1}{p r_2}t) + \\ & + h \sin(t + \frac{r_1}{r_2}t - \frac{r_1}{p r_2}t - \frac{r_1}{p r_3}t); \end{aligned} \]
Where \(r_1, r_2, r_3\) — are radii of the circles and \(p\) is the ratio of the path that the second circle traveled along with the first to the path that the third circle traveled along with the second one.
Overall, there are four parameters on which the final curve depends: the ratio of the radius of the first circle to the second \(k\), the ratio of the radius of the first circle to the third \(k_2\), the ratio of the paths \(p\), and the distance to the drawing point \(h\).
By changing parameters in real-time, we can observe how changing each parameter affects the final image.
4K 60fps rendering of this video took almost 6 hours. Consider subscribing to my Patreon to support this project and get this and other videos from this page in full quality.